Les enjeux de l’enseignement des mathématiques au CM2, année qui prépare au collège, sont considérables. Chantal Kritter et Françoise Cerquetti-Aberkane, agrégées de mathématiques et formatrices en ESPE, et Sylvia Caira, conseillère pédagogique référente mathématiques, ont minutieusement adapté le contenu à la fin de l’école primaire française (à Singapour, l’école primaire s’arrête à l’issue de la 6e).
Nous avons en outre demandé à deux mathématiciens d’en relire les épreuves, Mohamed Houkari, professeur de mathématiques à Henri IV, et Benoit Rittaud, enseignant-chercheur et maître de conférence à l’Université Paris 13 (Institut Galilée), afin de nous assurer que les contenus étaient bien conformes aux attendus de l’enseignement secondaire.
Quels enjeux au CM2 ?
L’année de CM2, telle qu’elle est enseignée à Singapour, pose les bases de l’enseignement de l’algèbre, et représente selon moi l’aboutissement de cette belle pédagogie des mathématiques, visuelle et concrète, préparée dès le CP.
Je vous en donne quelques exemples (parmi bien d’autres) :
La proportionnalité :
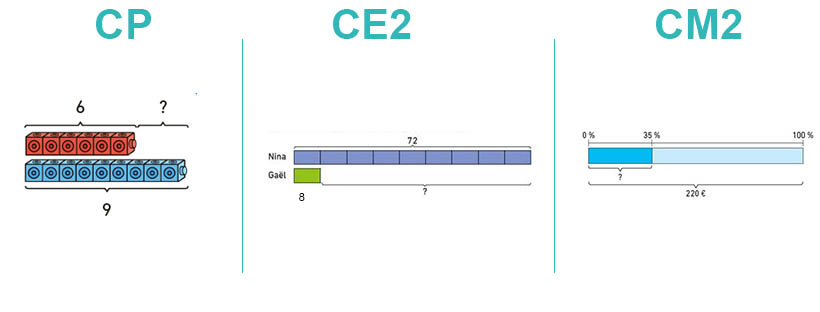
Dès le CP, les élèves se sont habitués à modéliser les problèmes à l’aide de schémas en barres. Ce sont d’abord de simples problèmes additifs (CP et CE1) puis multiplicatifs (CE2 et CM1) et fractionnaires (CE2, CM1 et CM2) ; au CM2, cette modélisation « en barres » permet aux élèves de comprendre tout naturellement la proportionnalité, à travers les notions successives de rapports (1 pour 2, 3 pour 4…), de taux (rapports entre deux quantités, tels que la vitesse, le débit, etc…) et de pourcentages (rapports de 1 pour cent). Habitués aux représentations visuelles, les élèves sont en mesure de résoudre des problèmes qui demandent aux élèves du système traditionnel de « poser un x » : préparation parfaite, donc, de l’algèbre, dont l’année de 6e marque le commencement.
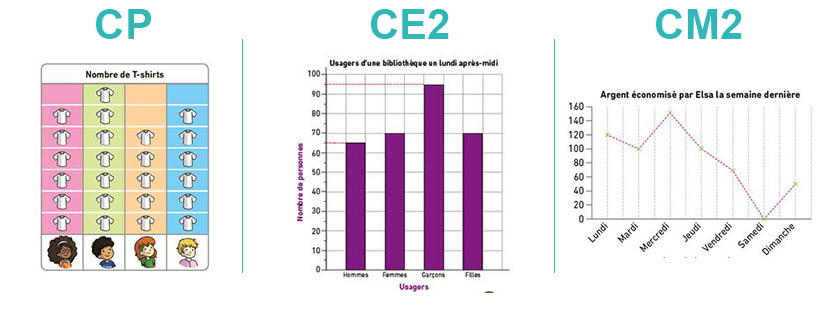
Les diagrammes : Dès le CP, les élèves qui suivent la méthode de Singapour, apprennent à représenter des données simples dans des tableaux, qui se complexifient au fur et à mesure des classes. Au CE1 puis au CE2, les tableaux permettent de représenter des rapports proportionnels de manière discrète puis continue (diagrammes en barres) ; au CM2, les diagrammes en barre deviennent des graphiques cartésiens et permettent de représenter des données de plus en plus fines.
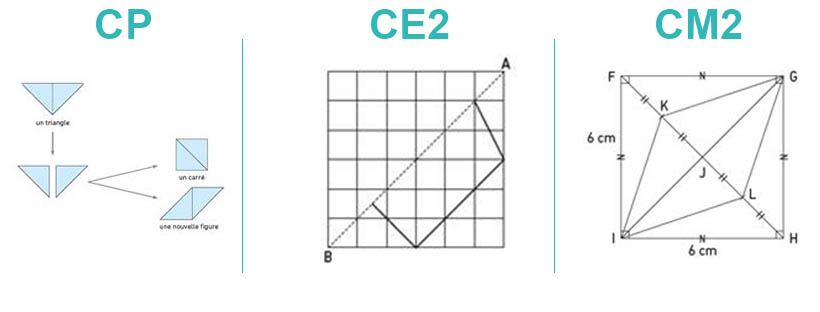
La géométrie : Le plus gros travail d’adaptation de la méthode de Singapour aux usages français a porté sur l’enseignement de la géométrie. En effet, la tradition française accorde une place prépondérante aux raisonnements géométriques et à la construction de figures. Grâce à la nature explicite et spiralaire de l’enseignement singapourien, les auteurs sont parvenus à restituer de manière particulièrement efficace et progressive cette tradition française tout en respectant les principes pédagogiques d’origine.
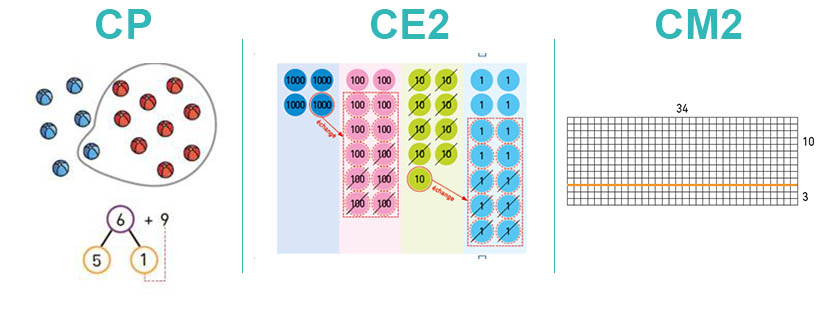
La numération : Puisque les élèves, dès le CP, ont appris à jongler avec les quatre opérations dans des situations variées, ils ont acquis une familiarité avec les nombres qui leur a permis d’automatiser les calculs, les tables, etc. Les procédures de calcul posé (principalement au Cycle 2) permettent aux élèves de comprendre ce qu’ils font et pourquoi ils le font : ils ont ainsi acquis, du CE1 au CM1, une grande aisance à poser des calculs complexes. Mais au CM2 – et c’est une autre originalité de la méthode de Singapour par rapport à la tradition française – les élèves passent beaucoup moins de temps à poser les calculs : ils se concentrent plutôt sur la résolution de problèmes et découvrent l’usage raisonné de la calculatrice. Certes, nous avons pris soin, dans notre adaptation, de rappeler les techniques de calculs posés (divisions et multiplications par des nombres à 2 chiffres) mais ce n’est clairement pas un objectif didactique privilégié par Singapour.
Un projet d’établissement, du CP au CM2
La raison pour laquelle j’insiste sur ces progressions, notion par notion, année après année, c’est que la parution du manuel de CM2 est pour moi l’occasion de reformuler un principe qui me tient à cœur : quelle que soit la méthode que vous choisissez en mathématiques, elle sera d’autant plus efficace qu’elle sera suivie du CP au CM2 au sein de votre établissement et en collaboration avec vos collègues.
Une bonne méthode, pour le dire simplement, c’est avant tout une bonne progression. Et c’est particulièrement vrai dans les matières complexes que sont le français et les mathématiques.
Et c’est selon moi le principal ingrédient du succès de la méthode de Singapour : chaque notion est introduite tôt (les quatre opérations dès le CP, les fractions dès le CE1, les aires dès le CE2, etc.) avec des situations simples, concrètes et accessibles aux élèves ; puis elle est revue et approfondie l’année d’après afin de permettre aux élèves de baigner d’emblée dans un univers familier, tout en se sentant progresser. Les concepteurs de la méthode ont anticipé, dès la première séance du CP, l’objectif fixé pour la fin de l’école primaire.
Cette progression cohérente, structurée, planifiée d’année en année a été éprouvée dans les écoles de Singapour, pendant près de quarante ans, et c’est dans cet esprit que nous travaillons depuis dix ans afin d’adapter la méthode aux programmes français.
Séance après séance
Ce n’est pas tout : nos auteurs, sous la direction de Dr. Monica Neagoy pour le Cycle 2 et de Chantal Kritter pour le Cycle 3, ont adapté chaque séance de la méthode de Singapour à votre année scolaire, afin que chacune des 180 heures annuelles dévolues par les programmes officiels à l’enseignement des mathématiques apportent à vos élèves le confort de cette progression rassurante, explicite et claire.
Dans nos guides pédagogiques, nous avons veillé à respecter (j’exagérerais peut-être en disant « minute par minute » !) cette progression fine, qui mêle de façon équilibrée manipulation, modélisation, raisonnement, objectivation et pratique autonome.
Nous avons également distillé des conseils pédagogiques et didactiques, explicité les concepts mathématiques, proposé des pistes de différenciation et des activités optionnelles afin que, dans le cadre structuré de cette progression, vous puissiez faire un usage éclairé de votre liberté pédagogique.
En lisant cela, vous vous dites peut-être « évidemment, c’est ce que font tous les éditeurs de manuels scolaires dans leurs guides pédagogiques ». Aussi je vous invite à feuilleter nos guides en ligne pour vous rendre compte par vous-même de la précision de l’accompagnement proposé, pensé pour répondre au mieux à la diversité de vos pratiques.
Pour faciliter votre mise en œuvre de la méthode, nous mettons intégralement en ligne nos guides pédagogiques et nos manuels, parce qu’il me semble essentiel que vous puissiez vous lancer dans la méthode en toute connaissance de cause.
Fixer la barre haut
Je sais que, la méthode de Singapour renvoie l’image d’une méthode exigeante, peut-être parfois déroutante.
Je ne veux pas contredire cette perception, et je l’assume : la méthode de Singapour demande de la part des professeurs qui l’utilisent un investissement professionnel certain. Comme le dit Dr. Monica Neagoy, nous « fixons la barre haut » parce que le challenge est le facteur principal de la motivation – pour vous comme pour vos élèves, et parce que le plaisir que procurent les mathématiques est proportionnel à l’effort intellectuel qu’elles demandent.
Mais nous avons aussi conscience de vos contraintes de terrain – le temps, l’hétérogénéité de vos classes, l’exigence des programmes, l’équipement en matériel pédagogique adéquat … nous travaillons sans cesse à améliorer, à simplifier, à expliciter les contenus pédagogiques de nos manuels.
Nous écoutons vos retours, les difficultés que vous rencontrez et nous nous rendons dans vos classes pour prendre en compte vos remarques.